Solving single line to ground fault using the MVA method

Although the ARCAD online short circuit calculator doesn't currently calculate unbalanced faults all in one run, you can still use it to resolve positive, negative and zero sequence SC MVA required to determine total line-to-ground MVA_F and I_F at point of fault. All you need is to develop hierarchical trees representing positive, negative and zero sequence networks of your power distribution system, program them into the calculator to determine the respective sequence short circuit MVA at prospective fault points. Short circuit current values for balanced three phase bolted fault as well as for unbalanced line-to-ground, line-to-phase etc. faults can be determined by converting the calculated SC MVA values to kA units.

The example below shows the technology behind solving single phase to ground fault using the MVA method. Figure 1 represent one line (part a) and MVA diagram (part b) of simple power distribution system.

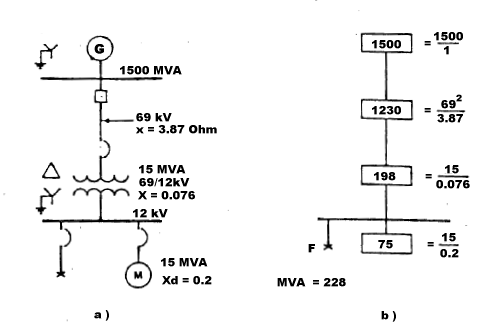
MVA sequence diagram below shows all components of positive, negative and zero sequence networks in SC MVA quantities. The connection shown illustrates ground fault at the 12 kV bus.

As noted, the three phase fault has been solved to be 228 MVA at the 12 kV bus. Since the positive sequence fault is equal to negative sequence fault, MVA_X1 = MVA_X2 = 228

The zero sequence fault MVA, however, must be calculated, and its MVA value then is combined with the positive and negative MVA values.

In our example, during a fault on the 12 kV bus only the transformer and the motor contribute to zero sequence MVA. The delta primary of the transformer blocks any zero sequence power flowing from the system and across the transformer. Therefore, Figure 2 shows the zero sequence power circuit:

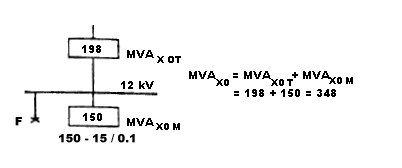
MVA_{X0 T} = MVA_{X1 T} = MVA_{X2 T} = 198 as the transformer zero sequence reactance equals its positive and negative reactance.

MVA_{X0 M} = 15 / 0.1 = 150 MVA, since the zero sequence reactance of the motor is about 1/2 of its positive sequence reactance. The total zero sequence fault power then is equal to the sum which is:

MVA_{X0 T} + MVA_{X0 M} = 198 + 150 = 348

The line to ground fault power is obtained with the use of Figure 3.

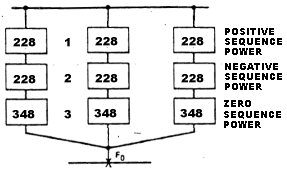
Since, these are three branches in parallel, the simplest approach is to solve MVA value for one out of the three circuits, and multiply the result by 3. Use formulas (1) or (2) to calculate total MVA of components with respectively equal or arbitrary X/R ration connected in series or parallel. Assuming equal X/R ratio: